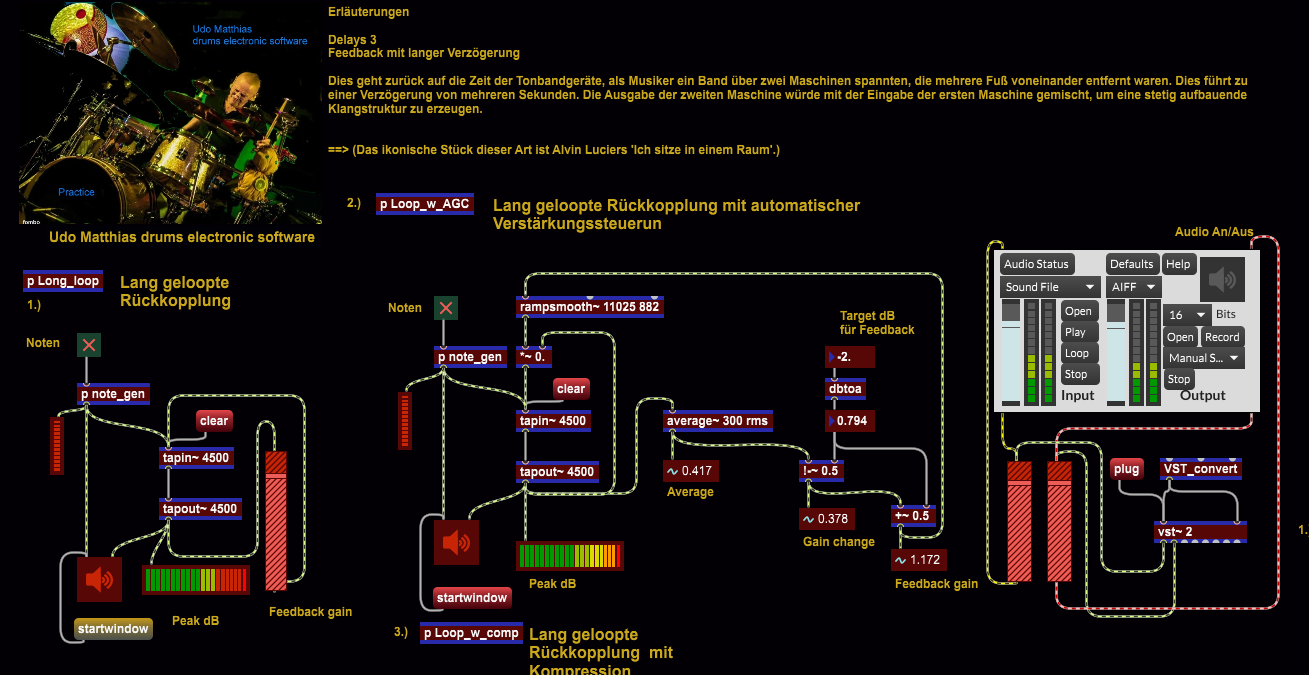
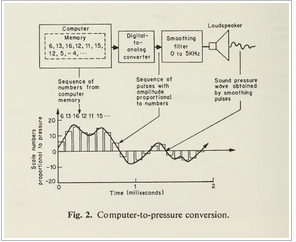
Zustandsmaschine Markov


Search!!
Blues-Set

Kategorien
Neueste Beiträge
- Irene Schweizer 26/07/2024
- Joe Morris 25/07/2024
- Eva Klesse 12/07/2024
- Oskar Sala 04/07/2024
- Chris Cutler 03/07/2024
- Stephan Emig 02/07/2024
- Ram Dass 27/05/2024
- Francis Stringbender 27/05/2024
- J.B. Bouvet 24/05/2024
- Release Music Orchestra 13/05/2024
- Gail Priest 11/05/2024
- Lisa Ann Schonberg 10/05/2024
- Peter Sculthorpe 08/05/2024
- Florian Arbenz 04/05/2024
- Otonality und Udonality 22/04/2024
Schlagwörter
Aarau (351)
Ableton (674)
Afrigal (836)
Afrika (674)
Anthony Braxton (444)
Art in general (336)
Basel (771)
Berliner Schule (402)
Bern (722)
Bruno Spoerri (429)
C++ (554)
Chuck (583)
ETH Zürich (675)
Experimentelle Musik (402)
Freiburg im Breisgau (667)
Hamid Drake (325)
Harry Lehmann (412)
Improvisierte Musik (347)
Jazz (425)
Jazz (198)
jimi hendrix (367)
john coltrane (510)
Kandern (730)
Karl Friedrich Gerber (490)
Klaus Weinhold (472)
Kraftwerk (490)
Kunst(neue)Musik (365)
Luzern (713)
Lörrach (745)
MAXMSP (681)
Müllheim (713)
Nebenau (743)
Neue Musik (579)
Peter Giger (486)
Pierre Favre (484)
Puredata (541)
Resin Binzen (673)
Rheinfelden (655)
Soundart (659)
Udo Matthias (635)
Udo Matthias drums/electronic/software (873)
Weil am Rhein (707)
Wilfrid Kirner Berlin (600)
Wollbach (661)
Zürich (755)
Seiten
- Ablaze Records
- afrigal udo matthias#1
- afrigal udo matthias#2
- afrigal udo matthias#3
- afrigal udo matthias#4
- afrigal udo matthias#5
- Afrika & Afrigal
- AI/KI Kunst Live Coding
- Avantgarde Electronic Experimental
- Coding //******
- Computer Music & Horror Vacui
- diverse Links
- Eigenes Afrigal
- Frank Zappa
- freie Improvisation
- Gedanken von mir und anderen
- generative art
- Hardware Hacking & Circuit Bending
- Improvisierte Musik
- index
- King Crimson
- Klanglandschaften
- Kunst, Raum & NEUE Musik
- Masterclasses
- Mir Folgen??
- modular&Co
- Musik Spiritualität Mystik Politik
- NEO Krautrock & Show me your Lips
- New Thing & History
- Psychoakustik – Skulpturale Klangphänomene
- Purchase Confirmation
- Purchase History
- Raritäten
- Rilke und anderes
- Schönberg & Kandinsky
- Soundart
- Sounds aus dem All
- start
- Tzolkin Maya
- Unterricht MAXMSP Chuck JAVA Assembler C+- Ableton Live
- Urbex
- Visualisierung
Zustandsmaschine Markov
Ente
Spacebox
AFRIGAL
Afrigal
Follow Me
Suche
Neue Beiträge
- Irene Schweizer 26/07/2024
- Joe Morris 25/07/2024
- Eva Klesse 12/07/2024
- Oskar Sala 04/07/2024
- Chris Cutler 03/07/2024
Archive
- Juli 2024
- Mai 2024
- April 2024
- März 2024
- Februar 2024
- Januar 2024
- Juli 2023
- Juni 2023
- Mai 2023
- April 2023
- März 2023
- Januar 2023
- Dezember 2022
- November 2022
- Oktober 2022
- September 2022
- August 2022
- Juli 2022
- Juni 2022
- Mai 2022
- April 2022
- März 2022
- Februar 2022
- Januar 2022
- Dezember 2021
- November 2021
- Oktober 2021
- September 2021
- August 2021
- Juli 2021
- Juni 2021
- Mai 2021
- April 2021
- März 2021
- Februar 2021
- Januar 2021
- Dezember 2020
- November 2020
- Oktober 2020
- September 2020
- August 2020
- Juli 2020
- Juni 2020
- Mai 2020
- April 2020
- März 2020
- Februar 2020
- Januar 2020
- Dezember 2019
- November 2019
- Oktober 2019
- September 2019
- August 2019
- Juli 2019
- Juni 2019
- Mai 2019
- April 2019
- März 2019
- Februar 2019
- Januar 2019
- Dezember 2018
- November 2018
- Oktober 2018
- September 2018
- August 2018
- Juli 2018
- Juni 2018
- Mai 2018
- April 2018
- März 2018
- Februar 2018
- Januar 2018
- Dezember 2017
- November 2017
- Oktober 2017
- September 2017
- August 2017
- Juli 2017
- Juni 2017
- Mai 2017
- April 2017
- März 2017
Schlagwörter
Aarau
Ableton
Afrigal
Afrika
Anthony Braxton
Art in general
Basel
Berliner Schule
Bern
Bruno Spoerri
C++
Chuck
ETH Zürich
Experimentelle Musik
Freiburg im Breisgau
Hamid Drake
Harry Lehmann
Improvisierte Musik
Jazz
Jazz
jimi hendrix
john coltrane
Kandern
Karl Friedrich Gerber
Klaus Weinhold
Kraftwerk
Kunst(neue)Musik
Luzern
Lörrach
MAXMSP
Müllheim
Nebenau
Neue Musik
Peter Giger
Pierre Favre
Puredata
Resin Binzen
Rheinfelden
Soundart
Udo Matthias
Udo Matthias drums/electronic/software
Weil am Rhein
Wilfrid Kirner Berlin
Wollbach
Zürich